There’s a machine in your facility whose motor fails every couple of years. Your job is to find out why. Conducting a root cause analysis of the failures is where to start. You need an understanding of the factors to consider in choosing the correct motor for the application so you can determine if the motor is the right one. If you know the major factors that could cause the motor to fail, you can check each in your application as you search for a solution.
Motor characteristics
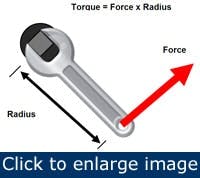
Figure 1. This conceptual graphic shows that torque exists, whether or not there is rotation.
We need to understand some of the characteristics of motors — torque, horsepower, current, service factor and load profile, among others. Motor horsepower is what we think of first, torque is next. The difference can be illustrated by imagining a wrench turning a shaft (Figure 1).
Torque is the turning force applied to the shaft. It doesn't matter if the shaft actually turns. Torque is measured in foot-pounds (ft-lb or lb-ft) and is independent of rotating speed. Now, if we let the torque turn the shaft, we introduce speed into the equation. This leads us to horsepower, which is how fast we are injecting work into the shaft. If we double the turning speed while keeping torque constant, we double the horsepower. By definition, the relationship between torque and horsepower is:
1 hp = 33,000 lb-ft/min.
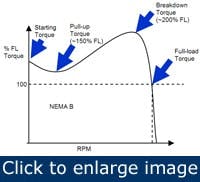
Figure 2. There are four important points on a motor’s speed-torque curve.
Figure 2 is a typical motor speed-torque curve. The one shown corresponds to a NEMA Design B motor, probably the most common in industry. There are several points on this curve we need to understand if we are to select a motor properly.
Full-load torque is the torque necessary to produce rated horsepower at full-load speed. It's equal to:
FLT = hp x 5,252/FLS
Where FLT = full-load torque (in ft.-lb.)
hp = rated horsepower
FLS = full-load speed (in rpm)
The locked-rotor torque, also called starting torque, is the torque applied to the shaft when power is first applied but before the motor starts to turn. Locked-rotor torque usually is expressed as a percentage of full-load torque.
Pull-up torque, also called accelerating torque, is the minimum torque developed during the period from locked-rotor condition to breakdown. It’s the minimum torque needed to accelerate the load from zero speed to running speed. It’s also the first critical selection factor. Pull-up torque is usually expressed as a percentage of full-load torque.
Breakdown torque occurs at the point where increasing load causes a rapid speed decrease. Consider a motor with a brake. As we apply the brake tighter and tighter, we reach a point where the motor slows to a stop. That's breakdown and it’s expressed as a percentage of full-load torque.
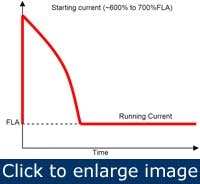
Figure 3. This is a graphical representation of the inrush current that flows when a motor first starts turning.
Motor current also is related to speed (Figure 3). There are two points of interest here. The first is full-load current, which is the steady-state current that flows when the motor is operating at full-load torque and speed. Locked-rotor current is the steady-state current through a motor with the rotor locked and with rated voltage applied. Operating at locked-rotor condition for more than 20 seconds can result in insulation damage because of excessive heat generation.
Service factor
Service factor is the permissible amount of overload a motor can withstand while remaining within defined temperature limits. When voltage and frequency are maintained at nameplate-rated values, the motor tolerates overload to the horsepower obtained by multiplying the rated horsepower by the service factor shown on the nameplate.
However, locked-rotor torque, locked-rotor current and breakdown torque are unchanged. Operating under these conditions will shorten motor life because of the higher temperatures, which causes the insulation to deteriorate more rapidly.
Motor temperature
Heat is a major consideration when selecting a motor. If the motor runs too hot, the insulation breaks down much faster unnecessarily. A common guideline states that each 10°C temperature rise above rated temperature cuts insulation life in half. High temperatures also can degrade the grease in the motor’s bearings, causing early bearing failure. Bearing or gear lubricant life is reduced by half for every 25°F (approximately 14°C) increase in temperature. The motor is subjected to two sources of heat: internal and external. The ambient temperature for the application should be expressed in degrees Celsius (°C). Most motors are designed to operate in an ambient of 40°C. If the ambient temperature is greater than that or the application requires frequent starting and frequent overloads, you should consider special motors to compensate for the increase in total temperature.
Motor cooling
The intent of motor cooling is to increase the rate of heat transfer from the motor to the surroundings, thus cooling the motor. Table 1 shows several ways of doing this.
| Motor enclosure | Enclosure type determines the airflow patterns over the motor. |
| Frame configuration | Ribbed housings have a larger surface area and, thus, transfer more heat. |
| Airflow |
Increasing the speed of the air flowing over the motor increases the cooling. |
| Ambient air density | Lower air density decreases the heat transfer. Most motors are rated to 3,300 ft. altitude. Motors with a service factor greater than 1.0 might be operated to 9,900 ft. at a 1.0 service factor. |
| Insulation class vs. temperature | Motor insulation is classified by NEMA for its ability to withstand high temperature. The total temperature is the sum of ambient plus motor temperature rise. If the motor has a temperature probe embedded in the insulation, the maximum temperature can be 10°C higher. |
Table 1. Common factors in cooling motors |
|
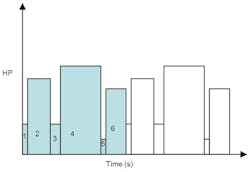
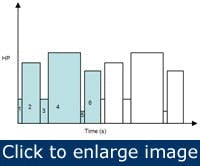
Figure 4. The demands on a motor can be variable, as illustrated by this representation of horsepower as a function of time.
Duty cycle Continuous duty implies that the load is essentially constant and might last for an indefinite time, usually many years. Intermittent duty means a repeating cycle of the motor being loaded for a period of time and then a period of unload or motor shutdown. In a varying duty cycle, the motor is subjected to a wide variety of loads (Figure 4).
Both peak and root-mean-square (RMS) horsepower are important variables. Use peak for selecting the motor torque, and RMS horsepower for selecting from a heating standpoint. RMS horsepower is the RMS average horsepower over the cycle. It’s calculated by making up a table (Table 2) with the peak horsepower and time for each step in the cycle.
| Step | Time (sec) |
hp | hp2t |
| 1 | 10 |
20 | 4,000 |
| 2 | 40 |
50 | 100,000 |
| 3 | 20 |
20 | 8,000 |
| 4 | 60 |
60 | 216,000 |
| 5 | 20 |
10 | 2,000 |
| 6 | 40 |
40 | 64,000 |
Table 2. Example data for calculating RMS horsepower |
|||
The right-hand column shows the square of the applied horsepower multiplied by the duration of that part of the cycle. Sum that column and the time column to learn that, for this example application, total time = 190 seconds and the sum of the individual values of hp2t = 394,000. These values suggest that:
RMS hp = sqrt(hp2t /t)
= sqrt(394,000/190)
= sqrt(2,074)
= 45.5 hp RMS
This implies selecting a motor of about 50 hp with a breakdown torque sufficient for the highest torque demand.
Multiple motor starts A special kind of duty cycle applies to a motor that performs repetitive starts with a given load and connected inertia. Motor selection must take into account the heating caused by repeated starting, load inertia and running load. The heating produced by a large locked-rotor (starting) current might limit the number of starts in a given period of time. During acceleration, a motor draws about 6 times the full-load current, so resistance heating losses (I2R losses) during starting can be 36 times the heating experienced at full load.
A motor operating on a low-inertia load (a pump, for example) might come up to speed very quickly, in less than one second. Starting losses might be so low that the entire cycle could be repeated several times per minute without overheating the winding. At the other extreme, the same motor connected to a high-inertia load (such as a large centrifugal blower) could burn out before getting up to full speed on the first start.
Other factors
Different types of braking can affect motor selection. A coasting stop or mechanical braking might affect the RMS horsepower calculation. Because plug stopping or DC braking uses the motor windings, they can develop considerable heat that must be taken into account.
Take the load into account when selecting a motor. This includes both the inertia of the driven machine and the load type. The inertia affects the time it takes the motor to come up to running speed, and thus affects heating. Depending on the type of driven machine, load type is classified as one of two main groups - constant torque or variable torque.
According to Newton’s Law, force is equal to mass times acceleration. In a rotating system, torque is equal to inertia times acceleration, or acceleration is equal to torque divided by inertia. To exhibit maximum load acceleration and minimum motor heating, the torque developed should be high with respect to the load’s inertia. NEMA publishes tables of external load inertia capability for various sizes of motors. Inertia (often indicated by the symbol W2K) is the rotary equivalent of mass. If we try to rotate a small flywheel, it won’t take much effort. But for a large flywheel, much more force (or torque) will be required.
If the system uses a speed changer (gears, pulleys, chains), the speed change ratio affects both the torque required and the reflected load inertia:
[pullquote]Tm = Tl/R
Ir = Il/R2
Where:
Tm = motor torque
Tl = load torque
R = speed ratio (motor rpm/load rpm)
Ir = reflected inertia
Il = load inertia
Load type
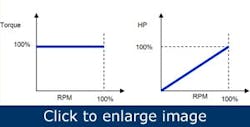
With a constant-torque load, the torque the load demands remains constant over the speed range of operation (Figure 5). Because horsepower is torque times speed (with a conversion constant), horsepower is directly proportional to speed (HP = torque x rpm/5,252) with constant-torque loads. This type of load is essentially a friction load such as conveyors, extruders or high-inertia loads. Shock loads and high overloads are sometimes classified as constant-torque. The most common case is when torque increases with increased speed (figure 6).
Figure 5. When a motor is operating at constant torque, the horsepower varies directly with speed.
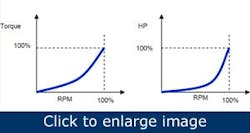
Figure 6. When a motor operates under variable-torque conditions, the linear relationship between horsepower and speed vanishes.
In variable-torque applications, however, the torque is proportional to the square of the speed and horsepower is proportional to the cube of speed (i.e. torque α RPM2 and hp α RPM3). Loads of this type might be a centrifugal pump, a fan or a blower.
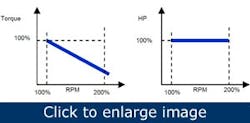
Figure 7. If a motor operates at constant horsepower, the torque developed is inversely proportional to speed.
Then there are constant-horsepower loads. These are variable-torque loads in which torque is inversely proportional to speed (Figure 7) while the horsepower remains constant and independent of speed. Machine tools and center-driven winders fall into this category.
To determine the type of load you have, you can use tables similar to those given in NEMA publication MG-1. Table 3 is an example.
| Load Description | Load torque as % of full-load | ||
| Breakaway | Accelerating | Peak Running | |
| Actuators |
|||
| Screw-down (rolling mill) |
200 | 150 | 125 |
| Positioning |
150 | 110 | 100 |
| Agitators | |||
| Liquid | 100 | 100 | 100 |
| Slurry | 150 | 100 | 100 |
| Blowers | |||
| Valve closed | 30 | 50 | 40 |
| Valve open | 40 | 110 | 100 |
| Positive displacement | 40 | 40 | 100 |
| Calendars, textile or paper |
75 |
110 | 100 |
Table 3. Characteristics of typical loads |
|||
Put it together
This brief list of motor-related variables should inform your decisions about root-cause analysis applied to machinery failures. Research each factor in detail if you decide it might contribute to your motor failures. And, there are other factors to consider, such as NEMA design and insulation class. Motors, if properly applied and maintained, should operate successfully for many years. If they don’t, don’t just keep replacing them with the same motor. Instead, perform a root cause analysis to find out why it failed.
The references in the sidebar were invaluable in researching for this article. You might find them useful, too. You probably can’t do too much to modify the load, but you certainly can change the motor to a more appropriate size or design.
James W. Taylor is director of operations at Machinery Management Solutions, Inc., Clarks Hill, Indiana. Contact him at [email protected] and (765) 366-4285.