Steam quality is a measure of the amount of saturated steam that coexists with its condensate in a given system. Calculate it by dividing the mass of steam by the total mass of steam and condensate.
Steam quality = Msteam/(Msteam + Mcond) (Eqn. 1)
Others have pointed out the importance of identifying steam quality in systems supporting industrial applications. For example, excessive moisture in the form of free droplets carried along with the main steam flow might impinge on turbine blades and cause mechanical damage. Likewise, high-velocity condensate can score valve seats and cause other erosion and corrosion related problems.
Ganapathy(1) gives a detailed explanation of how to calculate steam quality with a throttling calorimeter. A small quantity of the steam is throttled through an orifice from system pressure (PS) down to atmospheric pressure. The steam temperature at the orifice exit (TE) is recorded. This expansion is adiabatic. The following expression describes the energy balance associated with the throttling process:
HM = HL (1-X) + HGX (Eqn. 2)
And after rearranging:
X = (HL-HM)/(HL - HG) (Eqn. 2a)
Where:
HM
= enthalpy of superheated steam at temperature.
TE
= exit temperature at atmospheric pressure.
HL
and HG = the enthalpy of condensate and steam, respectively, at system pressure PS.
X
= the steam quality.
Thermodynamic data for calculating steam quality may be obtained from ASME Steam Tables(2) or any other library source(3). Ganapathy developed a diagram, which displays TE on the abscissa and X on the ordinate. A series of isobars for PS in the 50 to 500 psia range also is shown on the diagram. The diagram provides a quick estimate of steam quality when TE and PS are known.
Liley(4) calculated steam quality at pressures ranging from 2 bars (29 psia) to 20 bars (290 psia) in one bar increments. He developed an equation of the form:
X = A + BTE (Eqn. 3)
It describes the steam quality at each pressure, PS as a function of TE. Each set of coefficients A and B is valid for only a single pressure. Coefficients for pressures not included in the list must be interpolated. Solving equations 2a and 3 requires a user to look up recorded data.
The following equation was developed to quantify steam quality when the pressure and calorimeter temperature are known. It is valid for a steam quality between 0.95 and 1.00 and for pressures between 30 psia and 600 psia:
X = 0.9959 - 0.000442TE - ln[(PS + 6.8)0.03218(PS + 374)-0.0001581TE] (Eqn. 4)
Solving for TE:
TE = [0.9959 -X - 0.03218 ln(PS + 6.8)]/[0.000442 - 0.001581 ln(PS + 374)] (Eqn. 4a)
Expressing steam quality by means of a single continuous function eliminates the need for graphical data representation or interpolation. The equations can be used for online steam quality monitoring with a programmable process controller using orifice exit temperature and steam system pressure as input values, or they can simply be stored in the memory of a pocket calculator for use when the information is required.
By curve fitting available data in the ASME Steam Tables, the P-T relationship for saturated steam in the 30 to 600 psia range can be expressed as:
PS = 1.5 + (TS/120.62)4.5886 (Eqn. 5)
Solving for the saturated steam temperature TS:
TS = 120.62 (PS - 1.5)0.21793 (Eqn. 5a)
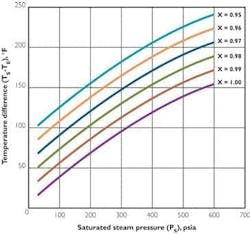
Substituting Eqn. 5 into Eqn. 4 allows the latter to be expressed entirely in terms of TE and TS. The graph in Figure 1 gives a quick method for calculating steam quality when saturation pressure and temperature and calorimeter temperature are known.
The validity of the above equations has been tested against a known example presented in one of the referenced articles and, at a more elevated pressure level, against steam data obtained from the Engineering Data Book(3).
The fast way
Try these examples
Example 1.
Calculate the steam quality of a 200 psia system when the orifice exit temperature is 250 F.
Liley, using the method described in his article, calculates the steam quality to be 0.9636. Applying Eqn. 4 with TE = 250 and PS = 200 gives an answer of 0.9649a difference of 0.13 percent.
Example 2
uses thermodynamic data obtained from the Engineering Data Book. It calculates steam quality at a pressure higher than that described in either of the two referenced articles:
Example 2. Calculate the quality of steam at 566.1 psia, when the throttling calorimeter temperature is 300 F.
The calculations use available data from the GPSA Engineering Data Book. At 566.1 psia, the enthalpy of the condensate is 464.5 Btu/lbm while the enthalpy of the saturated steam is 1204.1 Btu/lbm. The enthalpy of expanded steam at 300 F and 14.696 psia is 1,192.8 Btu/lbm. Substituting into Eqn. 2 gives: 1,192.8 = (1-X)(464.5) + 1,204.1 X. Solving for X yields 0.9840. Using Eqn. 4 instead results in an answer of 0.9836a difference of 0.004 percent.
Example 3.
Steam at 500 psia is to have a quality of not less than 0.9775. What should be the expanded steam temperature?
Eqn. 4a provides the answer. The calculated temperature is 289.5 F. This means the steam temperature at the orifice exit must be no less than 290 F.
Example 4.
A saturated steam system has a temperature of 460 F. Expansion in a throttling calorimeter results in a steam temperature of 300 F. Calculate the steam quality.
Start with Eqn. 5 to calculate system pressure when the temperature is 460 F. This gives a calculated pressure of 466.58 psia. This answer differs by 0.06 percent with the value noted in the Steam Tables. The calculated pressure and expanded steam temperature are then entered in Eqn. 4. The steam quality is 0.9844.
Example 5.
Calculate steam quality when saturated steam at 420 psia shows a temperature difference of 165 F between steam temperature and calorimeter temperature.
Use Eqn. 5a to calculate the saturated steam temperature: TS = 449.50 F. Then TE = 449.5 - 165 = 284.50 F. Now substitute PS = 420 and TE = 284.5 into Eqn. 4. Answer: X = 0.9756. Also refer to Figure 1 for comparison.
References:
(1) Ganapathy, V., "Calculate the moisture content of steam," Chemical Engineering, p. 127, August, 1993.
(2) Meyer, C.A., McClintock, R.B., Silvestri, G.J., and Spencer, R.C., Jr., ASME Steam Tables, 5th edition, A.S.M.E., New York, 1983.
(3) Engineering Data Book, Section 24, "Thermodynamic Properties," Revised 10th edition, Gas Processors Association, Tulsa, Oklahoma, 1994.
(4) Liley, Peter E., "A simple equation for steam quality," Chemical Engineering, p. 140, August, 1994.
Frank A. Rusche is a process engineer with Kellogg-Brown and Root in Houston, Texas. He can be reached at Frank.Rusche@Halliburton.com or 281-575-3432.
Figures: Kellogg-Brown and Root