Using air lift pumps or eductors for fluid handling
Ever since the Industrial Revolution, we've been searching for easier ways to get things done. Workers no longer stir smelly vats of wet nasties using nothing but a wooden paddle. They no longer form bucket brigades. Steam and electrical power boosted manufacturing productivity by multiple orders of magnitude.
One innovation was the retreat of the electrical motor from the point of action where fluids are being moved. It became possible to move fluids using an air lift pump or an eductor. Both devices operate effectively, in spite of the fact that neither has any moving parts.
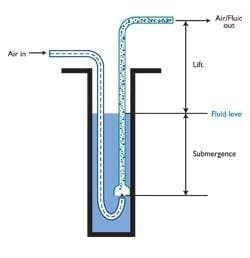
Figure 1. Schematic of an air lift pump
Air lift pumps
Air lift pumps serve two functions. First, they can eliminate fluid stratification in large unagitated tanks. Second, they can lift a liquid above its normal surface elevation without dilution and without introducing shear that damages fragile suspended solids.
In its most simple form, its construction consists of a vertical pipe, open on both ends (see Figure 1), that serves as a fluid pipe. A separate, smaller line, extends to the bottom of the fluid pipe and makes a U-turn. The open end extends a short distance into the bottom of the fluid line. When a compressed air starts flowing, rising bubbles transports slugs of fluid upward. The process is enhanced by the fact that bubbles also expand as they rise because the hydrostatic head is decreasing.
When used for agitating a stratified tank, the fluid pipe should be completely submerged to move material from the lower parts of the vessel to the upper sections. When used to lift fluid above its normal surface, the fluid pipe should be submerged only partially. As the two-phase flow reaches the top of the pipe, it overflows and the liquid disengages from the gaseous phase. The resulting highly non-uniform rate of overflow is collected to provide a more uniform flow for downstream gravity feeding or pumping.
Other applications include moving gritty and corrosive fluids that destroy metallic pumps, dewatering mine shafts, removing sediment from vessels and collecting samples from boreholes. The device also can be used in hazardous areas. Although the air lift pump can perform in-tank circulation quite efficiently, using it to raise a liquid becomes progressively more difficult as the elevation differential increases. At some point, it becomes simply more practical to use a motor-driven pump.
Because it's easier to remove contamination from air than it is to treat contaminated water, air lift pumps find a role in environmental remediation. As a result of the mass transfer and intimate, turbulent mixing of air and water, volatile organic materials in the aqueous phase are transferred to the gaseous phase as the material rises in the pipe. The EPA reports having used the technology to remove 1,1-dichloroethane and 94 percent of the trichloroethane present in the groundwater at a test site.
Sizing the air lift pump
The flowrate through an air lift pump is proportional to the flowrate of the air powering it. The literature reports air lift pump flow rates of 20 to 2,000 gpm and lifts to more than 700 ft.
| Lt (ft.) | C |
| 10-60 | 245 |
| 61-201 | 233 |
| 201-500 | 216 |
| 501-650 | 185 |
| 651-750 | 156 |
Table 1. Constant for use in air lift pump sizing equation. |
|
An empirical calculation attributed to the Ingersoll Rand Co. correlates the flow of air with that of water.
Va = 0.8 Ll/(C log10{(Ls + 34)/34]
Where Va = volume of free air (cu. ft.) needed per gallon of water
Ls = length of the submerged section (ft.)
Ll = length of the lift section (ft.)
C = constant that depends on Ll (see Table 1)
Another relevant variable is the relationship between Ls and Ll. Functional air lift designs exhibit a curious non-linear phenomenon. The ratio of submerged length to total length, Ls/(Ll + Ls), runs about 0.6 when the lift is only around 20 ft., but decreases to about 0.4 when the lift is 500 ft.
The last relevant variable is the air pressure needed to make the device operate. This depends, of course, on the specific gravity of the fluid. The depth that corresponds to one psi is inversely proportional to the specific gravity. For water, one psi corresponds to 2.31 ft. of depth. If one ignores the friction losses in the line, the applicable relationship is:
P = (Ls * sg/2.31)
Where
P = required gas pressure (psig)
sg = specific gravity of the fluid (dimensionless)
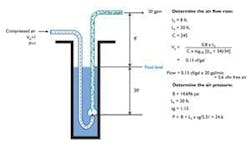
Figure 2. Sample air lift pump problem
To get some sense of scale, consider the pumping problem depicted in Figure 2. The desired flow rate is 20 gpm and the fluid in the tank has a specific gravity of 1.15. How much compressed air is needed and at what pressure? Refer to the calculations shown on Figure 2. For more information, refer to Clark, N.N. and Dabolt, R., "A General Design Equation for Air Lift Pumps Operating in Slug Flow", A.I.Ch.E. Journal, 32, No. 1, 1986 pp. 56-64.
Eductors
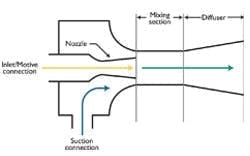
Another way to use a motive fluid to pump another is with an eductor. Also referred to as ejectors, exhausters or siphons, the eductor's principle of operation is straightforward (see Figure 3). The motive fluid (gas or liquid) enters the eductor with high initial velocity. As the high-speed jet passes through the nozzle, its pressure decreases in accordance with Bernoulli's theorem. The reduced pressure space pulls a gas, liquid or solid material through the suction port. After mixing, everything exits through the discharge port.
The applications for eductors are numerous. Installed near the bottom of a tank and fed with recirculated fluid from the tank, they effectively keep solids suspended. On the other hand, the same eductor can aerate the tank contents if it can aspirate air. Eductors can raise rainwater from underground vaults and secondary containment pits. They can blend liquids.
Other applications include evacuating a tank's vapor space and conveying light, finely divided solids or slurries. Fed with steam, an eductor can be used for heating fluids.
An eductor's performance can be controlled by modulating the motive fluid. Given a fixed suction pressure and suitable downstream measurement and feedback, the eductor can provide a stable vacuum or motive-to-suction flowrate ratio, which is useful for proportional feeding of two fluids.
Advantages to using eductors include low installation and maintenance cost. They can be fabricated or molded from any metal or plastic that's compatible with the fluids being moved. It is a self-priming design and can be used in hazardous areas.
The air lift pump and eductor are by no means obsolete technologies. They are in use every day in many plants. While they are not suitable for universal application, their unique characteristics will always provide them a place in the tools plants use for pumping and fluid handling systems.