From time to time, the plant professional is called upon to inspect or approve an industrial coating project. The material presented here should be of help to the engineer who needs to make sound decisions that can enhance coating performance. Expanded explanations of these principles can be found in SSPC’s Practical Math for the Protective Coatings Industry.
Film thickness and percent solids
When we say a coating has 65% solids, we usually mean 65% by volume. In other words, if 65% of each gallon is solids, the other 35% must be solvent that evaporates after application. If you spread the contents on a surface, the volume of dried paint would be 65% of a gallon. Because volume is equal to area multiplied by the thickness and the area covered by the wet paint is the same as the area covered by the dry paint, the thickness of the dry paint must be 65% of the thickness of the wet paint. For this coating, the dry film thickness (DFT) is 65% of the wet film thickness (WFT). If you need a DFT of 4.0 mils using paint that is 65% solids by volume, your WFT must be 4.0/0.65 = 6.15 mils. For a coating that is 100% solids, WFT and DFT are identical.
Dry film thickness per SSPC-PA 2
If two inspectors each measure DFT, they’ll most likely get different but similar numbers. Even if one inspector measures twice, the readings will differ. Different gauges also can indicate differently. Which measurement should determine if the specified DFT has been met?
According to SSPC-PA 2, the average of three gauge readings constitutes a spot measurement that must be reported with no more precision than the least precise single measurement. For example, the spot measurement for readings of 2.4, 2.6 and 2.9 mils is equal to 7.9/3 = 2.633 mils, which must be rounded to 2.6 mils.
SSPC-PA 2 specifies that a spot measurement shouldn’t be less than 80% nor more than 120% of the specified minimum DFT. Before starting your inspection, compute the upper and the lower limits for spot measurements so you’ll immediately know if the spot conforms to the specification.
The average of the spot measurements for a DFT specification with a minimum of 3.0 mils and a maximum of 8.0 mils must fall between 3.0 mils and 8.0 mils. An individual spot measurement can fall outside this range, provided it’s not too far outside. The exact limits are 2.4 mils (80% of 3.0) and 9.6 mils (120% of 8.0). As you inspect, every spot measurement between these two values is allowed. If you encounter a non-conforming spot, take additional measurements to determine the nonconforming area. Even though an individual spot measurement might outside the limits, the average must be inside.
The DFT for 100 sq. ft. is the average of five spot measurements made at random locations, according to PA 2. State the average with the same number of decimal places as the spot measurements.
Consider a specification that requires a DFT of 7.0 mils and the average of five readings (all of which are accurate to 0.1 mil) computed as 6.94 mils, it would need to be rounded to 6.9 mils, and wouldn’t meet the spec. On the other hand, if the spec said 7 mils, the 6.94 reading could be rounded to 7 mils, thus meeting the spec.
DFT can’t be specified to a precision that exceeds the precision of the available gauge. Even with a gauge that can read to the nearest 0.001 mil, surface irregularities may limit the precision of the measurement to the nearest 0.1 mil or even the nearest 1 mil.
Spreading rate
One gallon will cover 1,604 sq. ft. to a thickness of 1 mil. Consequently, a volume of 1,604 mil-sf is equivalent to one gallon. Determine the theoretical quantity of paint required for a project by using the following equation:
V = (A x D)/(1604 x P)
Where
V = theoretical volume of paint (gal.)
A = area to be covered (sq. ft.)
D = dry film thickness (mils)
P = percent solids (decimal value)
In practice, more paint is needed to account for application losses, waste in the can and non-uniform paint thickness.
Ventilation
The air flow through a containment or pollution detector is often specified in cubic feet per minute (CFM). When the cross-sectional area is constant, the flow rate is equal to that area times the air velocity. Consider a painting project covered by a rectangular containment that is 8 ft. wide, 10 ft. high and 60 ft. long. Assume you need a ventilating cross draft of 10 ft/min and can safely ignore leaks and frictional losses. Your cross-section area is 80 sq. ft., which when multiplied by the draft of 10 ft/min gives a theoretical fan capacity of 800 cfm. In practice, however, a larger fan would be required to account for losses.
Blast cleaning
A cleanly blasted steel surface can rust quickly before it gets painted unless the ambient relative humidity is kept low. But, blast cleaning requires a constant air flow to control dust. This means the ventilation air must be dehumidified before it can enter the work area. Because dehumidification equipment capacity is expressed in cubic feet per minute, sizing the unit for the job is easy.
For example, assume the project is blast cleaning a storage tank that is 90 ft. in diameter with a roof 6 ft. high and the specifications require two air changes per hour. Because two air changes are required each hour, the volume of air to be treated each hour is twice the tank volume. The tank volume is given by:
V = pi d[+]2[+] h/4
Where V = tank volume(cu ft)
d = tank diameter (ft)
h = tank height (ft)
In this case, the tank volume is 38,170 cu ft. and two air changes per hour correspond to an air flow of 76,340 cu ft per hour, or 1272 cfm. You’d probably want to round this up for safety reasons.
Humidity
Good painting practice dictates that the surface temperature of steel should be at least 5°F above the dew point during coating application to prevent moisture from condensing on the wet paint. Some zinc-rich coatings and moisture-cure polyurethane coatings require a minimum humidity to cure. Other coatings cure slowly in high humidity.
The temperature at which dew forms is called the dew point. Absolute humidity is a measure of the amount of water in the air. It’s usually measured as weight of water (grains) per unit volume of air (cu ft). Grain is a unit of weight having the abbreviation gr.
Historically, a grain was the weight of a grain of wheat, about 65 milligrams. Be careful not to confuse grains (gr) with grams (g).
Relative humidity (RH) is the ratio of the actual amount of water in the air to the maximum the air could hold. RH is a function of temperature and pressure, and is expressed as a percentage. Saturated air can hold no more water, and its relative humidity is 100%.
The temperature of the air closest to a steel surface, for example, in the bottom of the pits of the profile, will be equal to the temperature of the steel. If the temperature in the pit is slightly lower than the bulk air temperature, water can condense in the steel pit. That’s why the surface temperature should be greater than the dew point before paint application to provide a safety margin that avoids moisture condensation.
Hand-held electronic gauges have been developed that will measure surface temperature, air temperature and relative humidity. The device most commonly used to measure dew point and relative humidity is the sling psychrometer, which consists of two thermometers that are twirled through the air. The bulb of one thermometer is covered by a wet muslin cloth. As air movement causes the water in the muslin to evaporate, it absorbs heat from the bulb, thereby cooling the mercury in the wet-bulb thermometer. It will give a lower reading than the dry-bulb thermometer. This temperature difference is called the temperature depression and is used to find dew point and RH.
If the RH is low, water evaporates from the wet bulb quickly, resulting in a large temperature depression. When the ambient air is saturated, no water will evaporate and the two temperature readings will be the same, giving a temperature depression of zero.
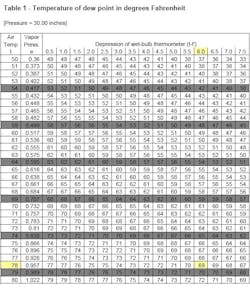
Psychrometric tables relate temperature depression to dew point and relative humidity.
They were first published by the U.S. government in 1900 and are now in the public domain. Copies can be obtained from suppliers of inspection equipment or can be downloaded from www.srh.noaa.gov/elp/psych/psych.html [no hyphens]. Because the formulas for computing these quantities are quite involved, the practical solution is to resort to tables.
Air pressure also affects dew point and relative humidity, so the tables are constructed for various atmospheric pressures (inches of mercury). The contemporary metric unit for pressure is the Pascal (Pa). One millimeter of mercury is equivalent to 133.32 Pascals. A pressure of one inch of mercury is equal to 3.386 kPa.
You can use this information to determine if ambient conditions are suitable for applying paint. For example, assume that conditions at a job site include a barometric pressure of 29.8 inches of mercury, an air temperature of 78°F, a wet bulb temperature of 72°F and a surface temperature of 81°F on the steel. What is the dew point? What is the relative humidity? Are conditions suitable for applying paint?
The first step is to compute the temperature depression of the wet bulb, which is 78°F - 72°F = 6°F. Because the tables are based on integer inches of mercury, use the tables for 30.0 in. of mercury. Enter Table 1 with the air temperature (78°F) and depression (6°F) to find a 69°F dew point.
Then, enter Table 2 with the air temperature (78°F) and depression (6°F) to find a 75% relative humidity. The difference between the surface temperature and the dew point temperature is 81°F – 69°F = 12°F, which is greater than 5°F, so the conditions are suitable for paint application.
This article is an excerpt from the book "Inspection of Coatings and Linings" and is used with the permission of SSPC: The Society for Protective Coatings, Pittsburgh PA. It appears here in an edited version.
Raymond E. F. Weaver is a mathematics professor and chair of the mathematics department at the Community College of Allegheny County—Boyce Campus.