Fuzzy logic deals with shades of gray

Overview

Fuzzy logic is the offspring of traditional expert systems and the fuzzy set theory developed and named by Lotfih Zadeh. An expert system evaluates inputs as either true or false. The underlying rules that generate outputs are based on the state of the inputs. The outputs may take the form of actions, decisions or intermediate conditions, which may be further processed as inputs in subsequent evaluations. Expert systems are limited, however, to input that can be evaluated as true or false. Its output is frequently binary, as well.

Imagine a problem that can be solved with logical rules and analog inputs. The question of whether the cup is half empty or half full illustrates the problem. Fuzzy set theory says that the partially filled cup can belong to both the sets of full cups and empty cups simultaneously. Each member of a fuzzy set has a property called the degree of membership that indicates the extent to which the member belongs. If the cup is full, it should be emptied. If it's empty, it should be refilled. What should be done when it's filled halfway? Or less? A traditional expert system would need many rules to deal with every possible state.

Enter fuzzy logic

Fuzzy logic invokes expert system-styled rules, but it can deal with shades of gray. Fuzzy variables reduce the number of rules to evaluate. Outputs are weighted according to the degree that inputs are "true."

Fuzzy logic is an excellent decision support tool. It more closely mimics human decision-making. People usually make decisions based on "fuzzy" inputs like warm and cool, big and small or fast and slow. A frequently cited example is a common bathroom shower. One doesn't need to know the exact temperature to decide whether the water is too hot. One doesn't need to know the flow rate to decide whether to increase it. If the flow rate and temperature are both unacceptable, we know intuitively how to adjust the valves.

Our thought process identifies simple rules to follow. If too hot, turn the cold water up and the hot water down. If the flow is too low, increase both hot and cold water. This is open loop feedback control. We might also make a large correction when the water is very hot and a smaller correction when water is barely too hot. The concept of using logical rules, but tempering the output based on inputs is the essence of fuzzy logic.

Fuzzy logic frames a control solution in terms of logical consequences. This characteristic is a double-edged sword. While it is suitable for many problems, its power comes from the rules. These are not easily generalized and the research and development in this technology becomes diluted with many one-of-a-kind solutions with limited opportunity for reuse. Clearly, there are notable examples where fuzzy logic has been demonstrated. The classic academic example is the inverted pendulum--a meta-stable system that's difficult to control for any feedback controller. Fuzzy logic is readily capable of keeping the inverted pendulum centered above the pivot point.

Examples

Another more practical example is crane control. The objective is to lift and move a large object to its destination, as quickly as possible. However, the object has mass and momentum can't be ignored. Movement must be controlled to prevent overshoot and swinging at the end of the movement. Fuzzy logic uses rules that maximize travel speed during most of the move, but decelerate the crane as the object approaches its destination. The load stops directly below the crane without swinging.

An example from the process industry is wastewater pH control. There are several ways to control pH using fuzzy logic, but the general premise is that rules control the addition of chemical on the basis of the current pH and how the pH has been changing with time. If the pH is far too high and a large dose of acid failed to correct it, then another, perhaps larger dose is called for. The amount of acid addition drops as the pH approaches the target.

Fuzzy vs. PID

PID feedback control is a simple, elegant design based on the deviation, or error, between a target value (set point) and the value of a process variable. An output, or manipulated, variable that affects the controlled variable is made to change. The output variable is usually a control valve or variable speed drive. Its signal is calculated from the magnitude of the error (proportional mode) the persistence of the error (integral mode) and the rate-of-change of the error (derivative mode).

In the early to mid 1970's, Mamdani investigated the fuzzy logic control as an alternative to the PID controller. He designed a controller that followed rules rather than a numerical formula. His rules were analogous to PI control. As a result, rules generated an output by evaluating error and change in error. For a reverse acting control loop, a large positive error calls for a large negative output change, while a small positive error calls for a small negative output change. Similarly, large change in error calls for large change in direction of the output, while a small change in error calls for a small change in direction. When there is no error or change in error, there is no change in output. This is an excellent application of fuzzy logic control because it's easily generalized to almost any process.

The rules can be represented in a truth table (see Sidebar). Note the symmetry of the outputs for these rules. The next issue is to define what constitutes a large error and large output. Membership functions are created for error, change-in-error and change-in-output. Mamdani defined five to seven membership functions for each variable. They were triangular in shape, symmetrical, evenly spaced and overlapping. Some experimentation was done with different numbers and shapes of membership functions, but the increase in complexity was not adequately rewarded by a performance improvement. However, the size and overlap of membership functions are tunable parameters analogous to conventional proportional, integral and derivative gains. Judicious selection of these fuzzy tuning parameters results in more or less aggressive control for a given process.

Some of Mamdani's students and colleagues picked up the torch and fuzzy logic control began to appear in cement kiln control, elevator speed control and automobile cruise control. One barrier to acceptance was the absence of a methodology for tuning the controller. Joe Qin improved on the Mamdani controller by simplifying it and showing how to tune it. The improved controller design offered benefits beyond ease of tuning. Simplifying the controller led to better performance.

This controller offers faster setpoint recovery with less overshoot than PID control for both setpoint changes and load changes. At the same time, it offers immunity to process noise when it is near setpoint because the controller develops a nonlinear response analogous to an error-squared PID controller. When the error is larger, the control action is larger than for PID; while when it is smaller, the control action is smaller. However, the nonlinearity is less severe than for an error-squared controller and robustness is not compromised. This controller is ideally suited for large time constants (not dead time) where overshoot and slow recovery are both undesirable. In fact, this controller generally outperforms PID loops in most situations.

Examples

Manufacturing carpets requires drying wet carpet from about 40 percent water to approximately four percent moisture. Carpet is pulled through a seven-zone oven. Each zone has two gas-fired burners and two overhead blowers. Both overdrying and underdrying damages the product, leading to waste or reprocessing. The oven operates continuously with different batches of carpet sewn end-to-end to avoid shutdowns. Temperature and speed targets are unique for each grade of product.

One batch can have significantly different weight and moisture load from the next. Transitions between grades present a difficult control problem. The operators knows where to target oven temperatures to achieve correct drying. The difficulty is getting the temperature controls to respond fast enough without overshoot. Oven temperatures can vary from 80 to 340º F, with setpoint changes as large as 100º F. Sometimes waste carpet is sewn between carpet batches to act as a buffer while temperature control stabilizes. This extra work reduces throughput.

A control system upgrade was justified with expectations of tighter control, improved product quality, increased efficiency, enhanced data collection and reduced rework. The burners and blowers remained the same. No changes were made to the oven. The only instrument upgrade was replacing the RTDs and connecting them to a Foundation Fieldbus system that replaced the single loop controllers. A new cabinet for the hardware was placed next to the existing one. Rewiring was easy. The burner control system was left intact and only the burner status wires had to be connected to the new controller. RTD inputs travelled on Foundation Fieldbus so the process could be monitored before implementing final changes. One at a time, the 4-20 mA outputs were disconnected from the single-loop controllers and reconnected to the new system. This only added about 3 ft. of shielded pair.

Wiring changes were made during weekends and zone-by-zone with zero downtime. In some cases, disconnected loops were reconnected to while running. Little training was needed. The system was configured with PID loops as a replacement in kind. Tuning parameters were copied from the old system and verified with an autotuner. Total time per loop was about 20 minutes; however, verifying final tuning had to wait for certain products to go through the line.

Unfortunately, PID control was incapable of meeting the expectations for improved control. So the PID controller was replaced with fuzzy logic. This reduced recovery time and eliminated transition overshoot. The fuzzy system was deployed only on the first zone, which has a tremendous impact on the entire oven. The burners in the first zone are larger and do most of the work. Configuration was simply a matter of changing the block from conventional PID to fuzzy. I/O, units and other parameters remained the same. The same autotuning function determined scaling factors. The improved control in the first zone stabilized the process so much that the PID loops in the other zones were left untouched.

The mill cited these benefits from fuzzy logic control:
· Elimination of product damage.
· Flexibility to make quick changes.
· Energy savings.
· Ease of operation.

The mill achieved documented gains of about 20 percent in capacity or throughput. Rework was eliminated completely. Actual payback was less than four months. Payback calculations did not include energy savings, which were also observed, but not quantified. Expectations were met and exceeded.

Fuzzy logic control is a valuable tool for control engineers. The generic version should be considered for processes when operators are able to outperform automatic controllers. The version analogous to PID can replace PID control in nearly any application, especially if overshoot is unacceptable. However, the difference in performance is related directly to the magnitude of the process time constants and to the magnitude of load or setpoint changes. This makes temperature control the most common candidate, particularly when grade changes or interrupting common resources create large step-like load swings.

Fuzzy theory

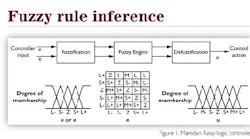
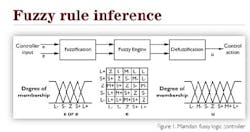
Fuzzy logic is executed in three steps. Fuzzification uses membership functions to transform analog variables into fuzzy variables. Membership functions can take on different shapes, but triangles are most common. The degree of membership varies from 0 to 100 percent as represented by the membership functions. In the Mamdani controller shown in Figure 1, membership functions for error and change-in-error have values of positive large, positive small, zero, negative small and negative large.