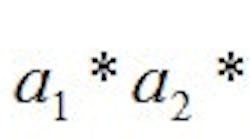Upon review of a number of balancing jobs within our facility, we identified a few critical issues. What started out as a random quality control audit of repair paperwork resulted in noticing that even on new motors, as well as on balanced motors when new sheaves and couplings were added, the rotors, sheaves and couplings tended to be out of balance tolerance. While this is not something new, especially with experience in the field indicating this same issue, many believe that because a component is new that it is in balance or that two components balanced separately will be within tolerance when run together.
Being the curious folk that we are, we decided to take a look under the hood and determine what the impact of the unbalance would be. The relationship between rotating equipment balance and bearing life is well documented and the impact can be approximated, especially assuming other conditions don’t change.
The question became: what is the impact of performing precision balancing on the reliability of a motor?
What is L10 life?
The most common method of referring to bearing life is to look at the point where 10% of the population of bearings fail. This is referred to the L10 life. The basic formula is fairly simple and is outlined in ISO Standard 281-2007, “Rolling Bearings — Dynamic Load Ratings and Rating Life,” as found in Equation 1. This relates to the theoretical L10 life assuming perfect conditions under identified load conditions.Equation 1RPM is speed, C is the dynamic load rating of the bearing, P is the effective load, and r is 3 for bearings and 3.333 for roller bearings. L10 is in hours.
This doesn’t give us enough data to calculate expected life from a given situation or based upon the maintenance or environment the machine is operating in. The result is that ISO Standard 281 includes tables, charts, and formulae to cover most of the additional issues such as different materials, life rating other than L10, lubrication, and environment. These are applied as shown in Equation 2.
Equation 2a1 is life adjustment other than 10%, a2 is for special materials, and a3 is for operating conditions and lubrication.
The a1 life adjustment is used for analyzing the expected percentage of failure of bearings beyond the 10% standard rating, as defined by ISO 281, Table 12 (Life modification factor for reliability).
Other factors identified include the approach to fatigue life limit, or speed limit, of the bearing, and load, or contact, stress. The adjustments for lubrication are also considered in the standard and can become quite intensive based upon the viscosity, additives, and type of bearing. Also considered is the environment that the bearing is operating in relative to the contaminants in grease. Multipliers are given in ISO 281, Table 13 (Contamination factor) represented in Table 1.
The P, or effective load from Equation 1, on the bearing is calculated several ways. One is the weight of the rotor on the bearings — basically, half the rotor weight across two bearings — and the rest are loads based upon other components attached to the shaft, unbalance, misalignment, belt tension, air gap eccentricity, and other conditions.
In effect, the calculation of bearing life can be as simple, but inaccurate, or complex, and accurate, as the analyst or engineer wishes. The primary purpose is to determine reliability. This can also be used as a way to determine the impact of different conditions. For instance, if we assume all other conditions are the same between bearings, we can change one condition and determine the overall impact of the L10.
We often hear of vibration in terms of mils (displacement), in./sec (or mm/sec — both are velocity) or g (acceleration). In the case of determining the amount of force due to unbalance alone, you need to determine the pound-inch (lb-in.) unbalance of the motor and attached components. This can be calculated as shown in Equation 3, where Flb is force in pounds.
Equation 3
Flb = 1.770*(rpm/1000)^2*lb-in.
Therefore, an 1,800 rpm rotor with 1/16 lb-in. unbalance and a diameter of 24 in. (12 in. radius) would have a radial force of 68.76 lb.
Figure 1. The rotor is actually vertically mounted with the result being that the bearings are larger in order to handle high axial thrust versus radial loading.
This force (Flb) is then multiplied against a constant that can be added to the forces calculated for the L10 life of the motor. In effect, the additional value to add to the weight of the rotor for P is Flb*1.333, or for the example above, P = 91.45 lb. If this rotor is 200 lb, then the life reduction can be calculated by comparing the bearing life before and after by adding the additional force for a second calculation and noting the difference.
Rotor example
The rotor shown in Figure 1 is actually vertically mounted with the result being that the bearings are larger in order to handle high axial thrust versus radial loading. For the purpose of this example, we will calculate the bearing life and impact based upon the rotor being horizontal and the load being primarily radial.
The rotor weighs 265 lb with a motor speed of 3,560 rpm. The bearings are each 6316 ZZ bearings with a C dynamic loading of 27,427 lb. The acceptable G2.5 unbalance, per the ISO 1940-2003 is 37 g-in., and the as-found was 98.3 g-in. Upon completion of balancing the final balance was 0.382 g-in. For purpose of the calculation, all information was converted to pound-inch (lb-in). The rotor is 8.25 in. in diameter, or 4.185-in. radius.
If we assume that conditions are such that an average bearing operates for five years in specific conditions and those conditions are the same when we compare the three different results, we have the following based upon the calculated L10 life.
Conclusion
As noted, the potential life for the bearings of an electric machine is significantly improved with precision balancing of the electric motor. With bearing failures making up more than 53% of motor reliability issues, balancing alone can improve the overall reliability of your system and, as a result, decrease your maintenance costs.